Sort Algorithm

05. 병합 정렬 (Merge Sort)

대표적인 ‘분할 정복’ 알고리즘으로, 평균 속도가 빠른 정렬 방식이다.

퀵 정렬의 경우 피벗 값에 따라서 편향되게 분할될 가능성이 있다는 점에서, 최악의 경우 비효율적으로 작동하는 알고리즘이었다. 그에 비해 병합 정렬은 정확히 반씩 나눈다는 점에서 최악의 경우에도 같은 효율성을 보장한다.

일단 반으로 나누고, 나중에 합쳐서 정렬하면 어떨까?

병합 정렬은 하나의 큰 문제를 두 개의 작은 문제로 분할한 뒤 각자 계산하고 나중에 합치는 방법을 채택한다.

즉, 기본 아이디어는 “일단 반으로 나누고, 나중에 정렬” 하는 것이다. 항상 반으로 나누고, 피벗 값이 없다.

/* 다음 배열을 오름차순으로 정렬하세요 */

21 10 12 20 25 13 15 22

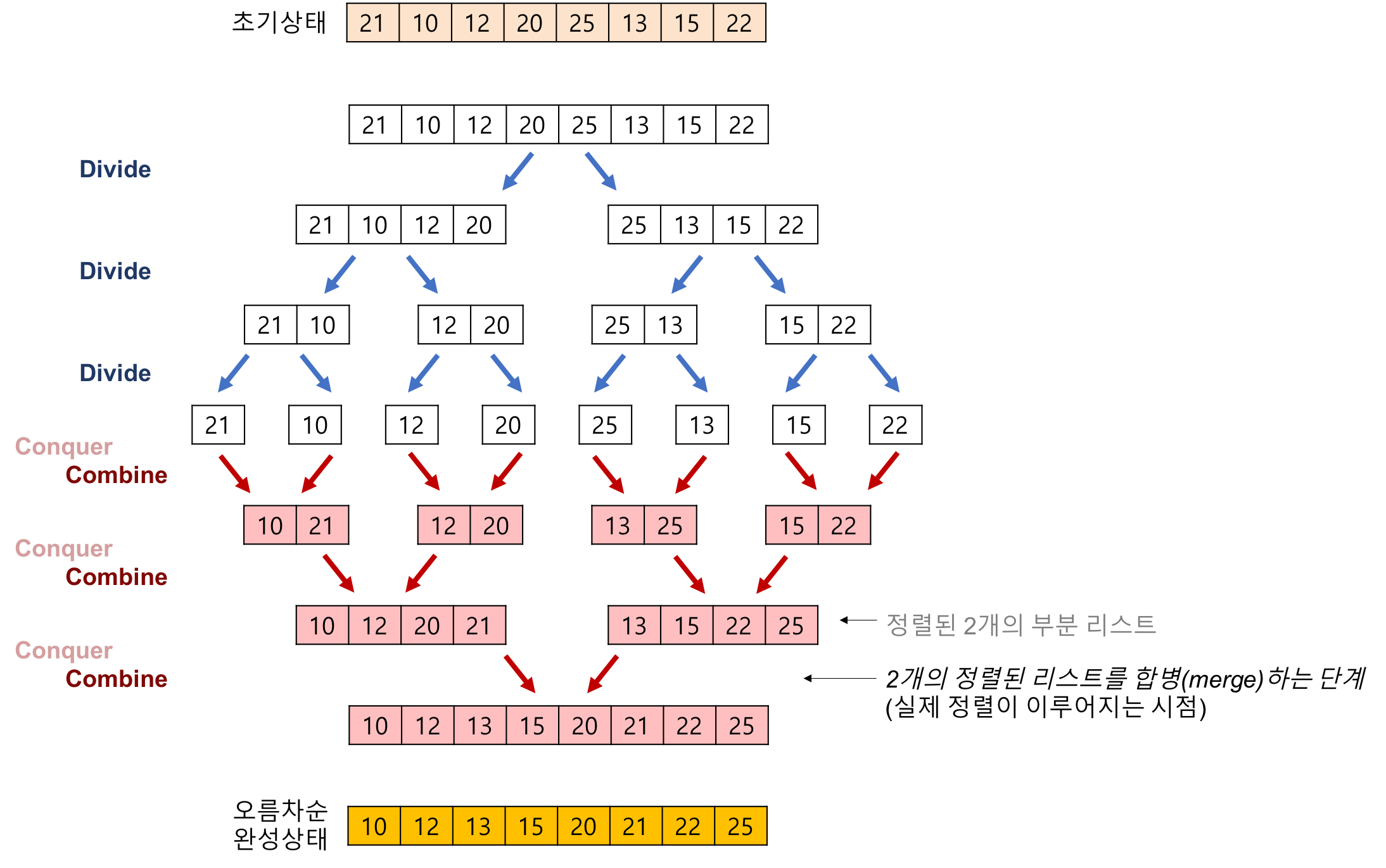
출처 : [https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html]

배열을 한 개의 원소만 있을 때까지 나눈다. 그 다음, 두 개씩 원소를 비교하면서 병합을 수행한다.

병합 정렬은 합치는 과정에서 실제로 정렬이 이루어지는 방식이다.

각 단계마다 부분집합 배열들이 이미 정렬되어 있는 상태이기 때문에 한 번씩만 읽어오면서 정렬할 수 있다.

Quick Sort에 비해 특별히 빠른 것은 아니지만, 최악의 경우라 할지라도 최소한 N*logN의 속도를 보장한다.

각 예시의 경우, 너비는 N, 높이는 logN 이다.

정렬에 사용되는 배열은, 반드시 전역 변수로 선언해야 메모리 낭비를 줄일 수 있다.

만약 함수 안에서 배열을 선언하게 되면, 매 번 배열을 선언하게 된다는 점에서 메모리 자원 낭비가 커질 수 있다.

이와 같이, 병합 정렬은 최소한의 속도를 보장하는 대신, 기존 데이터를 담을 추가적인 배열 메모리 공간이 필요하다.

Source code

#include <stdio.h>

int number = 8;
int sorted[8];	// 정렬 배열은 반드시 전역 변수로 선언

void merge(int a[], int m, int middle, int n) {
	int i = m;
	int j = middle + 1;
	int k = m;
	int t;
	// 작은 순서대로 배열에 삽입 
	while (i <= middle && j <= n) {
		if (a[i] <= a[j]) {
			sorted[k] = a[i];
			i++;
		} else {
			sorted[k] = a[j];
			j++;
		}
		k++;
	} 
	// 남은 데이터도 삽입
	if (i > middle) {
		for (t = j; t <= n; t++) {
			sorted[k] = a[t];
			k++;
		}
	} else {
		for (t = i; t <= middle; t++) {
			sorted[k] = a[t];
			k++;
		}
	}
	// 정렬된 배열을 삽입
	for (t = m; t <= n; t++) {
		a[t] = sorted[t];
	}
} 

void mergeSort(int a[], int m, int n) {
	// 크기가 1보다 큰 경우
	if(m <n) {
		int middle = (m+n)/2;
		mergeSort(a,m,middle);
		mergeSort(a,middle+1,n);
		merge(a,m,middle,n);
	} 
}

int main(void) {
	int i;
	int array[8] = {7,6,5,8,3,2,4,1};
	mergeSort(array, 0, number-1);
	for(i=0; i<number; i++) {
		printf("%d ", array[i]);
	}
}

시간 복잡도

병합 정렬의 평균 시간 복잡도 = O(N*logN)

깃허브