[Sort] 힙 정렬
Sort Algorithm
07. 힙 정렬 (Heap Sort)
병합 정렬, 퀵 정렬 만큼 빠른 알고리즘이다. 마찬가지의 시간 복잡도의 빠르기가 나온다.
고급 프로그래밍 기법으로 갈 수록 힙의 개념이 자주 등장하므로, 잘 알고 넘어가야 하는 알고리즘이다.
힙 정렬은 힙 트리 구조(Heap Tree Structure)를 이용하는 정렬 방법이다.
이진트리란 무엇인가?
이진 트리(Binary Tree)는, 각 노드(Node)를 두 개씩 이어 붙이는 구조를 말한다.
즉, 모든 노드의 자식 노드가 2개 이하인 노드를 말한다.
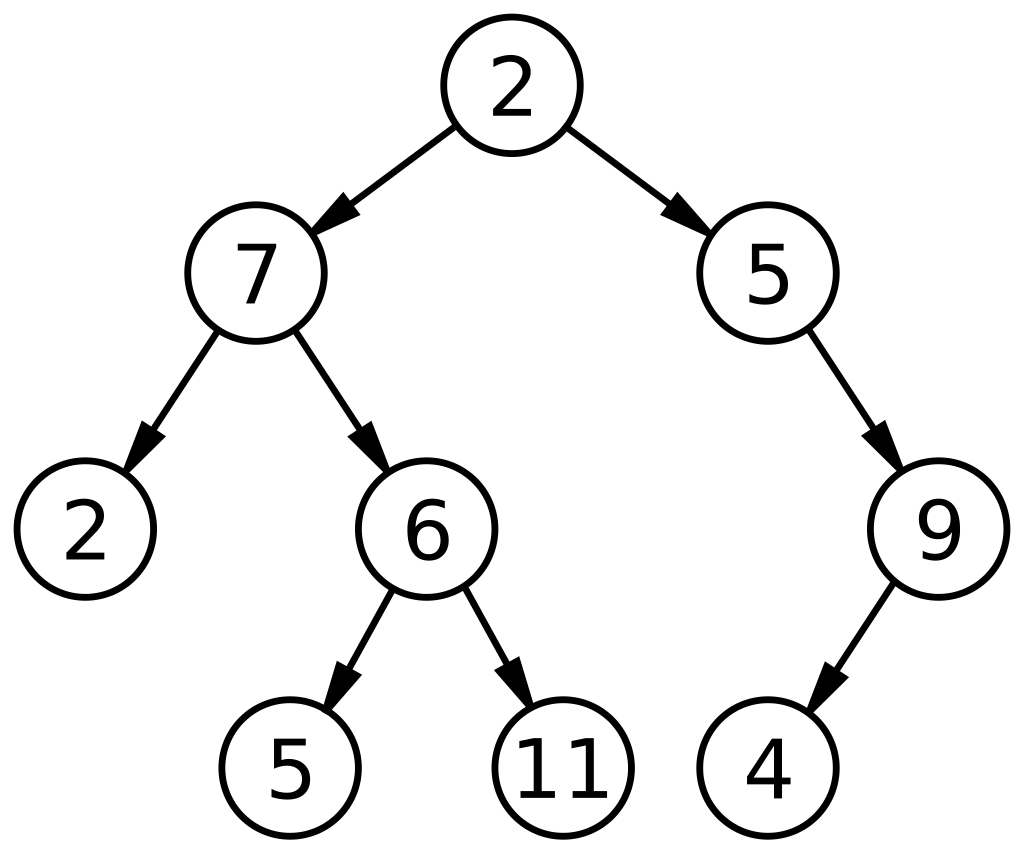
(출처: 위키)
위의 경우, 제일 상단에 위치한 2번 노드를 루트 노드(root)라고 한다. 제일 하단 즉, 자식 노드를 가지지 않은 마지막 노드들(2, 5, 11, 4)을 리프 노드(leaf)라고 한다.
완전 이진트리
트리에 자식 노드가 추가되는 순서가 가장 왼쪽부터 오른쪽으로 들어가는 방식을 완전 이진트리라고 한다.
힙
최솟값이나 최댓값을 빠르게 찾아내기 위해 완전 이진트리를 기반으로 하는 트리를 말한다. 힙에는 최대 힙과 최소 힙이 존재하는데, 최대 힙은 부모가 자식노드보다 큰 힙을 말한다. 힙정렬을 위해서는, 주어진 데이터가 힙 구조를 가지도록 만들어야 한다.
특정 노드 때문에 최대 힙이 붕괴되는 경우가 있다. 1번 부모와 자식 노드(2번 부모) 사이에는 최대 힙이 성립하지만, 2번 부모와 자식 노드(3번 부모) 사이에는 최대 힙이 성립하지 않는 경우이다. 이런 경우, 힙 정렬 수행을 수행하는데, 힙 생성 알고리즘(Heapify Algorithm)을 사용한다. 특정 ‘하나의 노드’를 제외하고는 최대 힙이 구성되어 있는 상태라고 가정하는 특징이 있다.
특정 부모 노드의 두 자식 중 더 큰 자식과 부모 노드의 위치를 바꾸는 알고리즘을 말한다. 또, 바꾼 뒤에도 자식 노드에 대해 자식이 존재하지 않을 때 까지 반복 수행해주는 알고리즘이다.
힙 정렬의 경우, 각 노드를 순서대로 index로 하여 배열로 선언해 준다. 그 후, 정렬하려는 숫자를 그대로 배열에 넣어 Heapify를 수행해주면 된다.
Source Code
#include <stdio.h>
int number = 9;
int heap[9] = {7,4,5,8,3,2,9,1,6};
int main() {
int i, c, root, temp;
// 먼저 전체 트리 구조를 힙 구조로 바꾼다.
for (i = 1; i < number; i++) {
c = i;
do {
root = (c-1)/2; // 부모 노드의 인덱스
if (heap[root] < heap[c]) {
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
c = root;
} while (c != 0);
}
// 크기를 줄여가며 반복적으로 힙을 구성
for (i = number-1; i >= 0; i--) {
temp = heap[0];
heap[0] = heap[i];
heap[i] = temp;
root = 0;
c = 1;
do {
c = 2 * root + 1;
// 자식 중에 더 큰 값을 찾기
if (heap[c] < heap[c + 1] && c < i -1) {
c++;
}
// 루트보다 자식이 더 크다면 교환
if (heap[root] < heap[c] && c < i) {
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
} while (c < i);
}
for (i = 0; i < number; i++) {
printf("%d ", heap[i]);
}
}
시간 복잡도
전체 트리에 대해서 Heapify를 수행하게 되면, 전체 노드가 힙 구조가 될 수 있다. **한 번 Heapify가 수행되는 시간은 트리의 높이와 같다**. 힙 구조는 완전 이진트리이기 때문에, 한 번 자식 노드로 내려갈 때마다 2배씩 증가한다는 점에서 log N이다. 따라서 전체 노드 N개에 대해 수행되는 시간은 N x logn 이다. 하지만, 실제로는 leaf 노드에서부터 위로 올라 갈수록 계속 1/2씩 줄어들기 때문에, 전체 노드의 절반만 수행해 주면 된다. 따라서 n에서 2를 나눈 N/2 x log N 이다. 하지만 N이 커질수록, log2N이 N/2 보다 작다는 점에서, O(N)에 가까운 속도도 낼 수 있다.
하지만 모든 경우가 다 해당이 되는 것은 아니므로, 평균적으로 힙 정렬의 시간 복잡도는 O(N x logN)이다.
병합 정렬과는 다르게, 별도의 추가 배열이 필요하지 않다는 점에서 메모리 효율성을 가진다.
또한 위 시간 복잡도를 항상 보장한다. 이론적으로 퀵, 병합 정렬보다 우위에 있다.
하지만 단순 속도만 가지고 비교하면 퀵정렬이 평균적으로 더 빨라서, 일반적으로 많이 사용되지는 않는다.
