Graph Algorithm

02. 깊이 우선 탐색 (Depth first search)

• 탐색할 때 깊은 것을 우선으로 하여 탐색을 수행하는 탐색 알고리즘
• 맹목적인 탐색 하고자 할 때 사용하는 방법
• Stack을 사용해 알고리즘이 수행된다.
• 기본적으로 컴퓨터 자체가 스택 원리를 사용하기에, 사실 Stack을 사용하지 않아도 구현 가능하다.
• 더 이상 인접한 노드가 없을 때까지 방문해서 해당 노드부터 거꾸로 거슬러 올라오며 탐색하는 방법

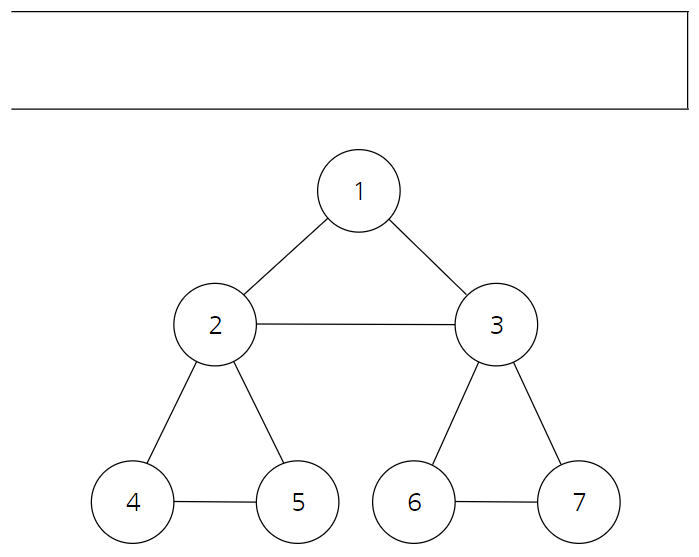
• DFS는 시작 노드(Start Node) 1을 Stack에 삽입하며 시작한다.
• 삽입한 노드들은 ‘방문 처리’ 해준다. (분홍색으로 표시)

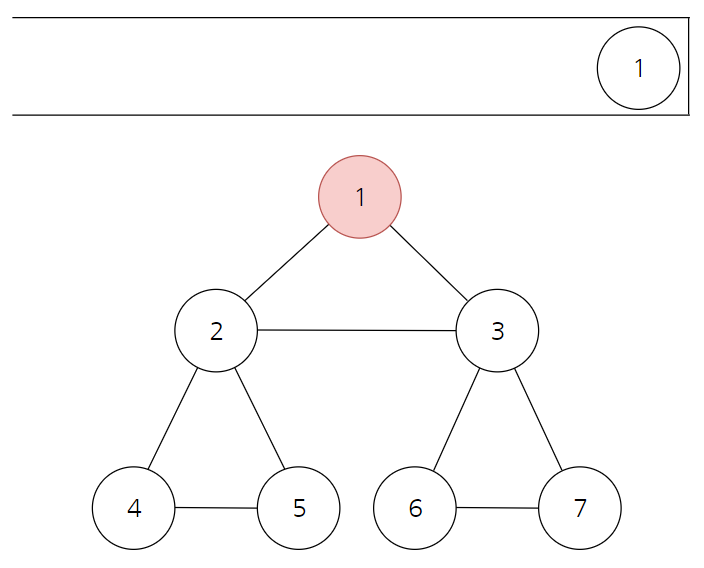
DFS는 다음과 같은 알고리즘에 따라 작동한다.

• 스택에서 제일 마지막에 들어온 노드를 확인한다.
• 스택의 제일 마지막 노드와 인접한 노드 중 방문하지 않은 곳이 있다면 그 노드를 스택에 넣고 방문처리 한다.
• 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 뺀다. (해당 노드가 탐색 되는 것)
• 위 과정을 반복수행한다.

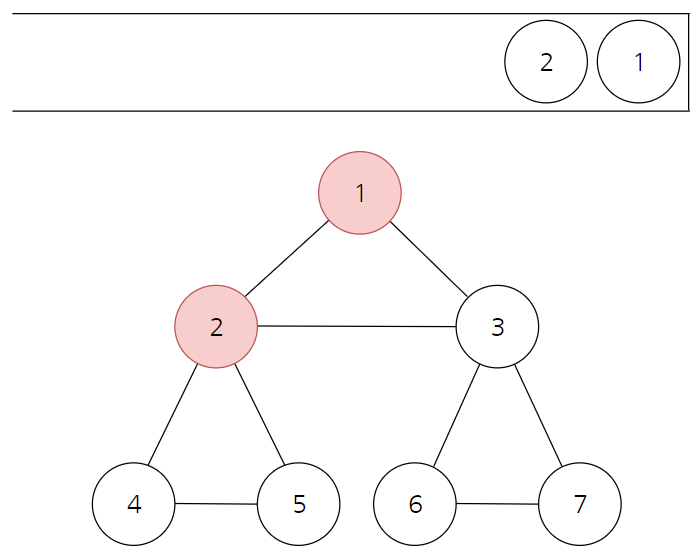
• 스택의 최상단 노드 1과 인접한 노드 2를 방문한 뒤 Stack에 삽입한다.

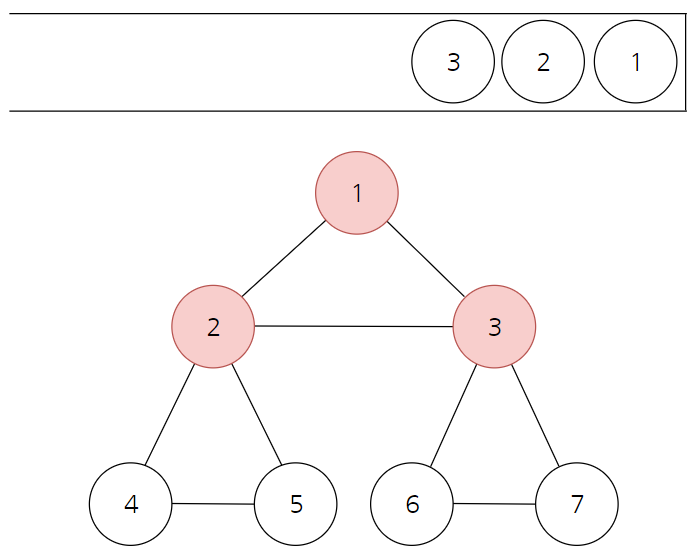
• 이어서 최상단 노드 2와 인접한 노드 3을 방문하고 스택에 삽입한다.

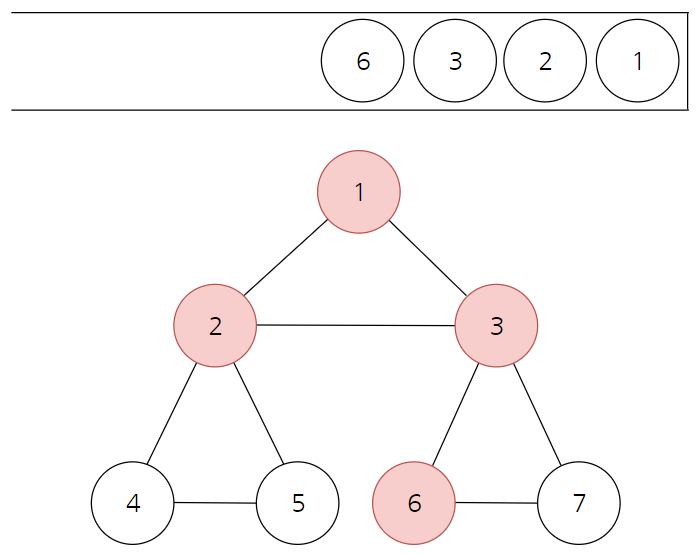
• 최상단 노드 3과 인접한 노드 중 방문하지 않은 6을 방문하고, 스택에 삽입한다.

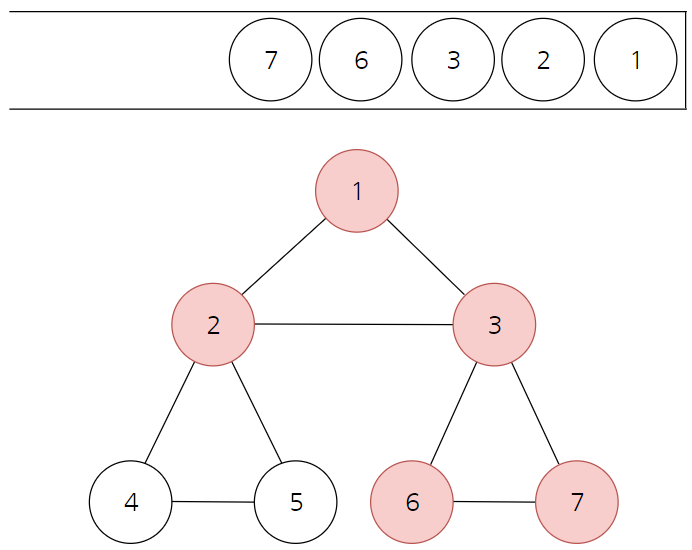
• 최상단 노드인 6과 인접한 노드 7을 방문하고, 스택에 삽입한다.

• 최상단 노드인 7에 더이상 방문하지 않은 인접한 노드가 없기 때문에, 7을 스택에서 뺀다. (7 탐색 완료)
• 다음 최상단 노드인 6과 3도 동일하게 수행해준다.
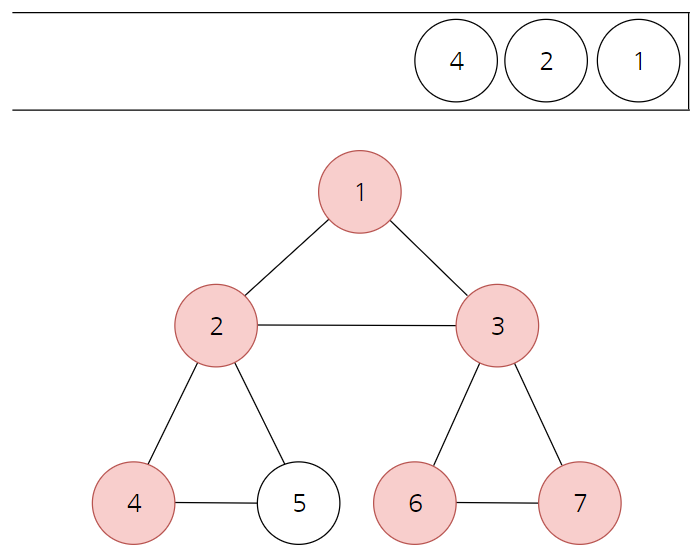
• 이어서 최상단 노드인 2와 인접한 노드 중 아직 방문하지 않은 노드 4를 방문하고, 스택에 삽입한다.

• 최상단 노드인 4와 인접한 노드 5에 방문하고, 스택에 삽입한다.

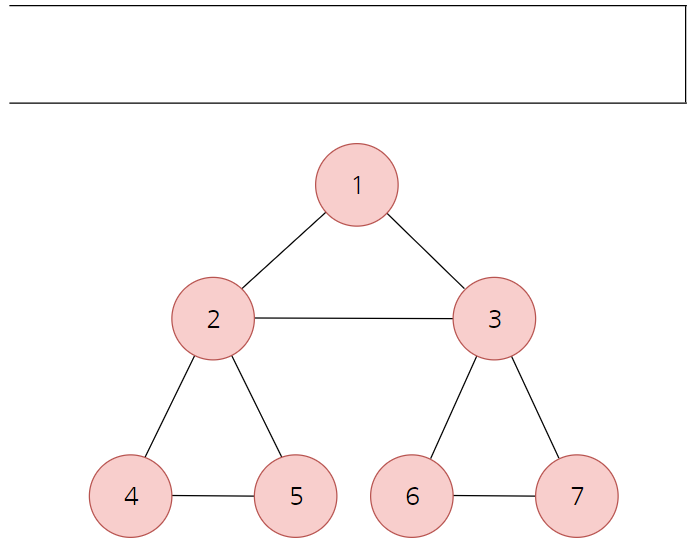
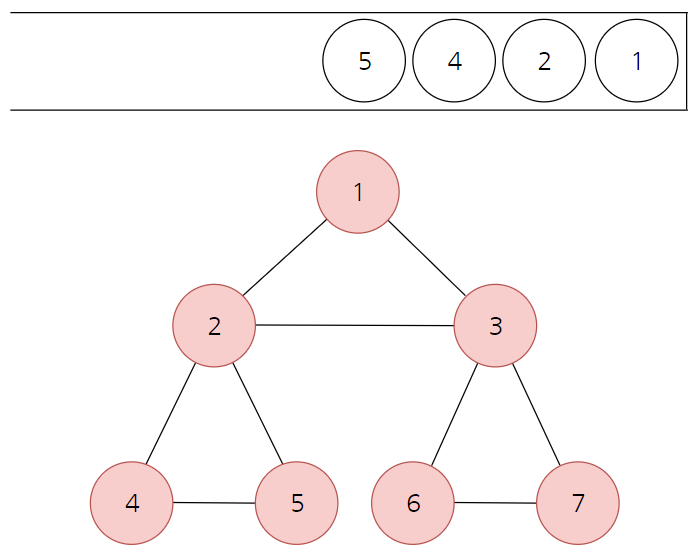
• 최상단 노드인 5에 더이상 방문하지 않은 인접 노드가 존재하지 않으므로, 스택에서 뺀다. (해당 노드 탐색 완료)
• 마찬가지로 스택의 최상위 노드들을 순차적으로 빼서 탐색을 완료한다.
• 따라서 방문 순서는 [1 - 2 - 3 - 6 - 7 - 4 - 5] 가 된다.

Source Code

#include <iostream>
#include <vector>

using namespace std;

int number = 7;
int c[8];
vector<int> a[8];

void dfs(int x) {
	if(c[x]) return;
	c[x] = true;
	cout << x << ' ';
	for(int i = 0; i < a[x].size(); i++) {
		int y = a[x][i];
		dfs(y);
	}
}

int main(void) {
	// 1과 2을 연결합니다. 
	a[1].push_back(2);
	a[2].push_back(1);
	// 1과 3를 연결합니다.
	a[1].push_back(3);
	a[3].push_back(1);
	// 2과 3를 연결합니다.
	a[2].push_back(3);
	a[3].push_back(2);
	// 2과 4을 연결합니다. 
	a[2].push_back(4);
	a[4].push_back(2);
	// 2과 5를 연결합니다.
	a[2].push_back(5);
	a[5].push_back(2);
	// 3와 6를 연결합니다.
	a[3].push_back(6);
	a[6].push_back(3);
	// 3와 7을 연결합니다.
	a[3].push_back(7);
	a[7].push_back(3);
	// 4와 5를 연결합니다.
	a[4].push_back(5);
	a[5].push_back(4);
	// 6과 7을 연결합니다.
	a[6].push_back(7);
	a[7].push_back(6); 
	// DFS를 수행합니다.
	dfs(1); 
	return 0;
}

DFS

• 수행 시간만 놓고 보면 Stack을 사용하는 것보다 재귀함수만 사용해서 구현하는 것이 훨씬 빠르고 안정적이다.
• BFS와 마찬가지로, 깊이우선 탐색의 방법이 다른 알고리즘에 적용이 되어 효과적으로 사용이 된다는 것 자체에 의미가 있다.
• 하나의 탐색 방법이기 때문에 이 자체는 큰 의미가 없다.
• 나중에 응용을 위해 개념을 배우는 것!

모든 자료 및 사진 출처

깃허브