Searching Algorithm

선형 자료구조

• 일직선 상에 나열된 자료구조로 배열, 스택, 큐 등이 있다.
• 이를 선형 자료구조라고 한다.

비선형 자료구조

• 위와 다르게, 일직선 상이 아니라 좌우 노드로 퍼져나가는 형태를 가진 자료구조를 비선형 자료구조라고 한다.
• 그래프, 트리 등이 대표적인 예시들이다.

• 그 중에서도 왼쪽 오른쪽 두 가지 경우로만 나뉠 수 있는 경우를 이진트리 라고 한다.
• 데이터의 탐색 속도를 빠르게 하기 위해 사용하는 구조이다. (힙 정렬에서 이진트리를 사용했었다)
• 그러나 완전 이진 트리를 사용했었기에 배열로 표현했지만, 완전 이진 트리가 아닌 이진 트리는 포인터를 사용한다.
• 그렇게 해야 더 효율적이고 유동적으로 트리 자료구조를 활용할 수 있다.

01. 이진트리 구현 및 이진 탐색 (Binary Search)

• 이진트리에서 데이터 탐색 기법은 크게 3가지로 나뉜다.

1. 전위 순회 (Preorder Traversal)

• 하나의 노드에 방문했을 때 다음 순서를 따른다.

  ​ (1) 먼저 자기 자신을 처리한다.

  ​ (2) 왼쪽 자식을 방문한다.

  ​ (3) 오른쪽 자식을 방문한다.

2. 중위 순회 (Inorder Traversal)

• 하나의 노드에 방문했을 때 다음 순서를 따른다.

  ​ (1) 먼저 왼쪽 자식을 방문한다.

  ​ (2) 자기 자신을 처리한다.

  ​ (3) 오른쪽 자식을 방문한다.

3. 후위 순회 (Postorder Traversal)

• 하나의 노드에 방문했을 때 다음 순서를 따른다.

  ​ (1) 먼저 왼쪽 자식을 방문한다.

  ​ (2) 오른쪽 자식을 방문한다.

  ​ (3) 자기 자신을 처리한다.

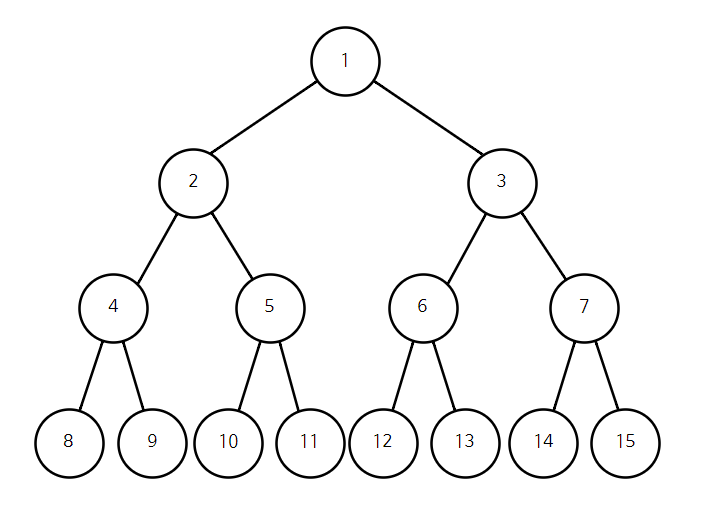
예시) 완전 이진트리의 방문 순서

• 전위 순회 이용
  • 1 - 2 - 4 - 8 - 9 - 5 - 10 - 11 - 3 - 6 - 12 - 13 - 7 - 14 - 15
• 중위 순회 이용
  • 8 - 4 - 9 - 2 - 10 - 5 - 11 - 1 - 12 - 6 - 13 - 3 - 14 - 7 - 15
• 후위 순회 이용
  • 8 - 9 - 4 - 10 - 11 - 5 - 2 - 12 - 13 - 6 - 14 - 15 - 7 - 3 - 1

Source Code

#include <iostream>

using namespace std;

int number = 15;

// 하나의 노드 정보를 선언합니다. 
typedef struct node *treePointer;
typedef struct node {
	int data;
	treePointer leftChild, rightChild;
} node;

// 전위 순회를 구현합니다.
void preorder(treePointer ptr) {
	if(ptr) {
		cout << ptr->data << ' ';
		preorder(ptr->leftChild);
		preorder(ptr->rightChild);
	}
}

// 중위 순회를 구현합니다. 
void inorder(treePointer ptr) {
	if(ptr) {
		inorder(ptr->leftChild);
		cout << ptr->data << ' ';
		inorder(ptr->rightChild);
	}
}

// 후위 순회를 구현합니다.
void postorder(treePointer ptr) {
	if(ptr) {
		postorder(ptr->leftChild);
		postorder(ptr->rightChild);
		cout << ptr->data << ' ';
	}
} 

int main(void) {
	node nodes[number + 1];
	for(int i = 1; i <= number; i++) {
		nodes[i].data = i;
		nodes[i].leftChild = NULL;
		nodes[i].rightChild = NULL;
	}
	for(int i = 1; i <= number; i++) {
		if(i % 2 == 0)
			nodes[i / 2].leftChild = &nodes[i];
		else
			nodes[i / 2].rightChild = &nodes[i];
	}
	preorder(&nodes[1]);
	return 0;
}

• 포인터를 이용해 구현하기 때문에, 꼭 완전 이진 트리가 아니더라도 안정적으로 동작한다.

시간 복잡도

이진탐색 기법의 시간 복잡도는 O(log n) 이다.

모든 자료 및 사진 출처

깃허브