Dynamic Programming

• 컴퓨터적 사고력을 물어보기 매우 적합한 알고리즘이다.
• 하나의 문제는 단 한 번만 풀도록 하는 알고리즘을 말한다.
• 예를 들어 일부 분할 정복 기법의 경우, 동일한 문제를 다시 푼다는 단점을 가진다.
• 대표적인 예시로 피보나치 수열이 있다.

피보나치 수열

• 1 1 2 3 5 8 13 …
• i번째 숫자를 구하기 위해 i-1과 i-2의 합을 구하는 수열이다.
• 피보나치 수열의 점화식 : D[i] = D[i - 1] + D[i - 2]

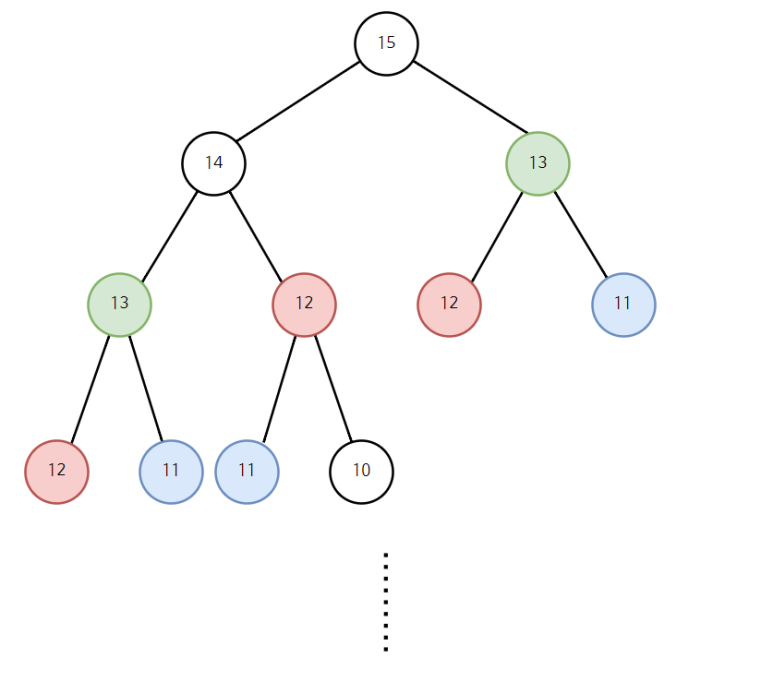
• 위 이진트리를 예를 들어보자.
• 노드 15의 값을 구하려면 14와 13을 구해야 한다.
• 14와 13도 각각 값을 구하려면 13과 12, 12와 11을 구해야 한다.
• 이런식으로 높이가 n이라고 치면, 한 칸 내려갈 때마다 구해야 할 값이 2배씩 증가하게 된다.
• 따라서 위 경우, 병합 정렬처럼 단순 분할 정복 기법을 사용하면 O(2^n) 수준으로 시간 복잡도가 커지기에, 매우 비효율적일 수 있다.
• 게다가, 이미 구한 값을 또 다시 반복 계산을 하는 경우가 매우 많이 생겨 비효율적이다.

다이나믹 프로그래밍 특징

• 다음 가정을 만족할 때 사용 가능하다.
  • 큰 문제를 작은 문제로 나눌 수 있다.
  • 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.

• 즉, 큰 문제가 있으면 그것을 잘게 나누어서 해결하고, 전체의 답은 나중에 구하는 방식이다.
• 이 과정에서, 이미 계산한 결과는 배열에 저장함으로써 나중에 동일 계산을 할 때 단순히 값을 반환만 하는 방법을 사용한다.
• 위 방법을 ‘메모이제이션(Memoization)’이라고 한다.

Source Code 1

#include <stdio.h>

int d(int x) {
	if(x == 1) return 1;
	if(x == 2) return 1;
	return d(x - 1) + d(x - 2);
}

int main(void) {
	printf("%d", d(10));
}

• 피보나치 수열을 예로 들어 확인했다.
• 하지만 이 경우, 분할 정복을 이용한 재귀호출이기 때문에 시간복잡도는 O(2^n)이 된다.
• 따라서 x 값이 커지면 기하 급수적으로 커지기 때문에, 해당 코드를 수행하는데 정말 오랜시간이 걸린다.
• 예를 들어 x에 50을 넣으면, 2^50 즉, 1,000,000,000,000,000개가 넘는 계산량을 컴퓨터가 처리해야 하는 것이다.

Source Code 2

#include <stdio.h>

int d[100];

int fibonacci(int x) {
	if(x == 1) return 1;
	if(x == 2) return 1;
	if(d[x] != 0) return d[x];
	return d[x] = fibonacci(x - 1) + fibonacci(x - 2);
}

int main(void) {
	printf("%d", fibonacci(30));
}

• 위와 같은 방법을 사용하면, 계산된 결과는 d 배열에 저장된다.
• 따라서 한 번 이미 계산이 되었다면 다시 계산이 수행될 필요 없이, 값만 반환하면 된다.
• 위 연산의 시간 복잡도는 O(n)으로 확 줄어들게 된다!
• 즉, 구해야 하는 노드의 높이(n)만큼만 계산하고, 나머지 값은 이미 계산이 진행된 배열에서 값만 반환하기 떄문이다.

모든 자료 및 사진 출처

깃허브